125 câu trắc nghiệm Số phức cơ bản !!
- Câu 1 : Cho hai số phức z1 = 3i - 2; z2 = 5 + 3i. Tìm số phức z = z1 + z2.
A. 3 + 6i
B. 9 - i
C. -1 + 10i
D. 4 + 3i
- Câu 2 : Cho số phức z = a + bi và . Mệnh đề sau đây là đúng?
A. w là một số thực
B . w = 2
C. w là một số thuần ảo.
D. w = i
- Câu 3 : Cho hai số phức z1 = 2 - 3i; z2 = 4i - 10. Tìm số phức z = z1 – z2.
A. z = 3 + 3i.
B. z = 12 - 7i.
C. z = 2 - 3i.
D. z = 3 - i.
- Câu 4 : Tìm số phức z thỏa mãn 3z - 3i = 6 - 9i
A. z = -1 + 2i
B. z = -3 + 2i
C. z = 1+ i
D. z = 2 - 2i
- Câu 5 : Cho số phức z = 10i - 8. Tìm phần thực, phần ảo của số phức w = z - i
A. Phần thực bằng -8 và phần ảo bằng -8i
B. Phần thực bằng -2 và phần ảo bằng -3
C. Phần thực bằng 8 và phần ảo bằng 10i
D. Phần thực bằng – 8 và phần ảo bằng 9
- Câu 6 : Cho hai số phức z1 = 3i - 4; z2 = 3 - i. Tìm số phức z = z1 – z2.
A. 6 - 5i
B. 7 + 4i
C. 4 + 4i
D. -7 + 4i
- Câu 7 : Cho hai số phức z = i. Tìm số phức w = z5.
A. w = i.
B. w = -1.
C. w = 1.
D. w = -i.
- Câu 8 : Cho hai số phức z1 = 1 + i; z2 = 1 - 2i. Tìm số phức z = z1.z2.
A. z = 1.
B. z = 3 - i.
C. z = -1 + i.
D. z = -2 + i.
- Câu 9 : Cho 2 số phức z1 = 2 + 2i; z2 = 4 - 5i .Tìm phần ảo của số phức w = z1.z2
A. 4.
B. -1.
C. -2.
D. 1.
- Câu 10 : Cho hai số phức z1 = 1 - i; z2 = 5 - 2i . Tìm phần ảo của số phức
A. b = -4.
B. b = 8.
C. b = 0.
D. b = -21.
- Câu 11 : Cho hai số phức z1 = 1 + i; z2 = 4 - i. Tim số phức
A. z = 2 + 8i.
B. z = 2 - 8i.
C. z = 5 + 3i.
D. z = 3 + 3i.
- Câu 12 : Tìm phần thực của số phức
A. 3/5.
B. 8/5.
C. 6/5.
D. Đáp án khác.
- Câu 13 : Tìm số phức
A.
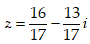
B.
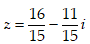
C.
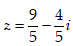
D.
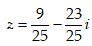
- Câu 14 : Tìm số phức z thỏa mãn
A.
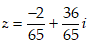
B.
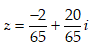
C.
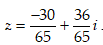
D.
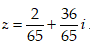
- Câu 15 : Tìm số phức
A.
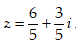
B.
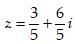
C.
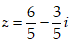
D.
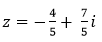
- Câu 16 : Cho số phức z = 6 - 8i. Tìm số phức
A. w = -3 + 2i.
B. w = 2 + 2i.
C. w = -2 - 2i.
D. w = 2 - 2i.
- Câu 17 : Cho số phức . Tìm số phức
A. w = -1 + 4i.
B. w = 9 - 2i.
C. w = 4 + 7i.
D. w = 4 - 7i.
- Câu 18 : Tìm số phức z thỏa mãn
A. z = 3 - i.
B. z = -3 - i.
C. z = 3 + i.
D. z = -3 + i.
- Câu 19 : Tìm số phức z thỏa mãn (1 + i)z + (2 - 3i)(1 + 2i) = 7 + 3i.
A.
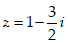
B.
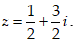
C.
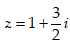
D.
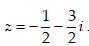
- Câu 20 : Tìm phần thực a của số phức z thỏa mãn (1 + i) 2( 2 - i) z = 8 + i + (1 + 2i) z.
A. a = 2.
B. a = -3.
C. a = -2.
D. a = 3.
- Câu 21 : Tìm số phức z =(2 - i) 3 - ( 2i + 1) 2
A. z= -5 + 15i.
B. z = 5 - 15i.
C. z = 3 - 8i.
D. z = 3 + 8i.
- Câu 22 : Cho số phức z = (1 - i) ( 2i - 8) . Tìm số phức
A. w = 10 - 10i.
B. w = -3 - 3i.
C. w = 16 - 16i.
D. w = -16 - 16i.
- Câu 23 : Cho số phức z = ( 2 + i)( 3 - i). Tìm phần thực a và phần ảo b của số phức
A. a = 7 ; b = 1.
B. a = 7 ; b = -1.
C. a = - 7; b = 1.
D. a = -7; b = - 1.
- Câu 24 : Tìm số phức liên hợp của số phức
A.
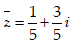
B.
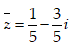
C.
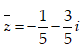
D.
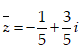
- Câu 25 : Tìm số phức z thỏa mãn
A. z = -3 - i.
B. z = -2 - i.
C. z = 2 - i.
D. z = 2 + i.
- Câu 26 : Cho số phức . Tìm phần thực a và phần ảo b của số phức
A. a = 2; b = 6.
B. a = -2; b = -6.
C. a = -2; b = 6.
D. a = 2; b = -3.
- Câu 27 : Tìm số phức liên hợp của số phức
A.
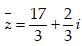
B.
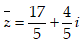
C.
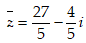
D.
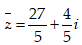
- Câu 28 : Tìm tổng phần thực và phần ảo của số phức z thỏa mãn
A. 13.
B. – 3.
C.10.
D. -10.
- Câu 29 : Tìm các số phức z thỏa mãn và
A. z1 = -1 + i; z2 = 1 - i.
B. z1 = 1 + i; z2 = -1 - i.
C. z1 = -1 + i; z2 = -1 - i.
D. z1 = 1 + i; z2 = 1 - i.
- Câu 30 : Cho số phức z = ( 3 - 2i)(1 + i) 2 . Môđun của là
A.2.
B.
C. 1.
D.
- Câu 31 : Cho số phức z thỏa mãn điều kiện . Môđun của số phức W = 1 + 2z + z2 có giá trị là:
A. 10.
B. -10.
C. 100.
D. -100.
- Câu 32 : Cho số phức z = -3 + 2i. Tính P = |z + 1 – i|.
A. P = 4.
B. P = 1.
C.
D.
- Câu 33 : Cho hai số phức z1 = 3 - 2i; z2 = -2 + i Tính P = | z1 + z2|.
A. P = 2.
B.
C. P = 1/2.
D. P = 2.
- Câu 34 : Cho hai số phức z1 = 3 + i; z2 = 2 - i. Tính P = | z1 + z1 z2|.
A. P = 10.
B. P = 50.
C. P = 5.
D. P = 85.
- Câu 35 : Cho số phức z thỏa mãn điều kiện: . Phần ảo của số phức w = 1 - iz + z là
A. 1.
B. -3.
C. -2.
D. -1.
- Câu 36 : Tìm phần thực, phần ảo của số phức z thỏa ( – i)(1 - i) = ( 1 + i) 3979
A. Phần thực là 21990 và phần ảo là 2.
B. Phần thực là - 21990 và phần ảo là 2.
C. Phần thực là -21989 và phần ảo là 1.
D. Phần thực là 21989 và phần ảo là 1.
- Câu 37 : Cho số phức z thỏa z = 1+ i+ i2+ i3+...+ i2016. Khi đó phần thực và phần ảo của z lần lượt là
A. 0 và -1.
B. 0 và 1.
C. 1 và 1.
D. 1 và 0.
- Câu 38 : Giá trị của biểu thức S = 1+ i2+ i4+ ...+ i4k là
A. 1.
B. 0.
C. 2.
D. ik.
- Câu 39 : Cho số phức z = 1+ ( 1+ i) + ( 1+i) 2+ ...+ (1+ i) 26 . Phần thực của số phức z là
A.
B.
C.
D.
- Câu 40 : Cho số phức z = x + y.i thỏa mãn z3 = 2 - 2i. Cặp số là(x;y)
A. (2; 2).
B. (-1; -1).
C. (3;-3).
D. (2; -3).
- Câu 41 : Cho số phức z = 3 + i. Điểm biểu diễn số phức 1/z trong mặt phẳng phức là:
A.
B.
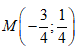
C.
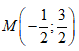
D.
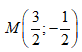
- Câu 42 : Gọi A là điểm biểu diễn của số phức z = 3 + 2i và B là điểm biểu diễn của số phức w = 2 + 3i. Trong các khẳng định sau, khẳng định nào đúng?
A. Hai điểm A và B đối xứng nhau qua trục tung.
B. Hai điểm A và B đối xứng nhau qua gốc tọa độ O.
C. Hai điểm A và B đối xứng nhau qua đường thẳng y = x.
D. Hai điểm A và B đối xứng nhau qua trục hoành.
- Câu 43 : Cho số phức z thỏa mãn iz + 2 - i = 0. Khoảng cách từ điểm biểu diễn của z trên mặt phẳng tọa độ Oxy đến điểm M(3;-4) là:
A.
B.
C.
D.
- Câu 44 : Tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện |z – (1+ i)| = |z + 2i| là đường nào sau đây?
A. Đường thẳng.
B. Đường tròn.
C. Elip.
D. Parabol.
- Câu 45 : Tìm tập hợp những điểm M biểu diễn số phức z trong mặt phẳng phức, biết số phức z thỏa mãn điều kiện
A. Tập hợp những điểm Mlà đường thẳng có phương trình 4x + 2y + 3 = 0.
B. Tập hợp những điểm M là đường thẳng có phương trình 4x - 2y + 3 = 0.
C. Tập hợp những điểm M là đường thẳng có phương trình 2x + 4y - 3 = 0.
D. Tập hợp những điểm M là đường thẳng có phương trình 2x + 4y + 3 = 0.
- Câu 46 : Tập hợp các điểm M biểu diễn số phức z thoả mãn |z – 2 + 5i| = 4 là:
A. Đường tròn tâm I(2 ; -5) và bán kính bằng 2.
B. Đường tròn tâm I(-2 ; 5) và bán kính bằng 4.
C. Đường tròn tâm I(2 ; -5) và bán kính bằng 4.
D. Đường tròn tâm O và bán kính bằng 2.
- Câu 47 : Cho z là số phức thỏa mãn là số thuần ảo. Tìm khẳng định đúng
A.
B. |z| = 1
C. |z| = 2
D.
- Câu 48 : Cho số phức z thỏa mãn là số thực. Khẳng định nào sau đây sai
A. z là số thực.
B. z là số ảo.
C. |z| = z.
D.
- Câu 49 : Cho các số thực a; b; c và d thỏa mãn: a+ bi= ( c+ di) n. Tìm khẳng định đúng
A. a2 + b2 = 2( c2 + d2) n
B. a2 + b2 = c2 + d2
C. a2 + b2 = 2n( c2 + d2)
D. a2 + b2 = ( c2 + d2)n
- Câu 50 : Tính tổng modul của các số phức z thỏa mãn z2 + |z| = 0
A. 1.
B. 2.
C. 3.
D. 4.
- Câu 51 : Có bao nhiêu số phức z thỏa mãn:
A. 1.
B. 2.
C. 3.
D. 4.
- Câu 52 : Có bao nhiêu số phức z thỏa mãn: z2 + |z| = .
A. 1.
B. 2.
C. 3.
D. 4.
- Câu 53 : Tìm các số phức z thỏa mãn:
A. z = 0
B.
C.
D. Tất cả đúng.
- Câu 54 : Tìm phần thực của số phức z thỏa mãn
A. 0.
B. 1.
C. 3.
D. 4.
- Câu 55 : Giải phương trình sau đây (2 + i)z = z + 2i - 1
A. z = 1 + i.
B. z = + i.
C. z = 2+ i.
D. Đáp án khác.
- Câu 56 : Tìm tổng phần thực và phần ảo của số phức z thỏa mãn: (1 - i) ( z - 2i) = 2 + i.
A. 4.
B. 3.
C. 5.
D. 7.
- Câu 57 : Giải phương trình sau đây :
A. z = 2.
B. z = -1.
C. z = -i.
D. z = 2i.
- Câu 58 : Tính tổng phần thực và phần ảo cùa số phức z thỏa mãn điều kiện sau:
A. 15.
B. 20.
C. 23.
D. 27.
- Câu 59 : Phần thực của số z thỏa mãn phương trình: (5 - 4i) z = ( 3 + 2i)(4 - i) gần với giá trị nào nhất.
A. 1,21.
B. 1,22.
C. 1,23.
D. 1,24.
- Câu 60 : Phần ảo của số z thỏa mãn phương trình: ( z + 2)i = ( 3i - z)( -1 + 3i) gần với giá trị nào nhất.
A. 2,11.
B. 2,21.
C. 2,31.
D. 2,41.
- Câu 61 : Cho phương trình sau: .Tính tổng tất cả các phần thực của các nghiệm của phương trình.
A. 2
B. 3
C. 4
D. 5
- Câu 62 : Cho số phức z thỏa mãn ( 3+ i) z = 2. Tính mô-đun của số phức w = z + - i.
A. 1.
B. 2.
C.
D.
- Câu 63 : Cho số phức z thỏa mãn điều kiện . Tìm phần thực của số phức w = 4z
A. 7.
B. 8.
C. 10.
D. 11.
- Câu 64 : Cho số phức z thỏa mãn hệ thức: . Tính mô-đun của z.
A. 3.
B. 4.
C.
D.
- Câu 65 : Tìm nghiệm của phương trình
A.
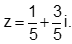
C.
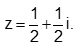
B.
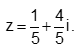
D.
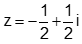
- Câu 66 : Tìm nghiệm của phương trình
A.
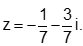
B.
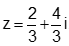
C.
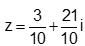
D.
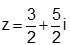
- Câu 67 : Tìm nghiệm của phương trình:
A. z = 1; z = i.
B. z = -1; z = i.
C. z = -i; z = 1.
D. z = -1; z = -i
- Câu 68 : Tìm nghiệm của phương trình
A. z = 1
B. z = i
C. z = -i
D. z = 2
- Câu 69 : Tìm nghiệm của phương trình
A. z = 2i
B. z = 1 + i
C. z = i
D. z = 2 + i
- Câu 70 : Tính tổng các phần ảo của các số phức z thỏa mãn phương trình
A. 0.
B. 1.
C. 2.
D. 4.
- Câu 71 : Cho số phức z thỏa mãn: . Tìm khẳng định đúng?
A. Có 2 số phức z thỏa mãn.
B. các số phức đó là số thực.
C. Các số phức đó là số ảo.
D. Tất cả sai.
- Câu 72 : Có bao nhiêu số phức z thỏa mãn z2 = | z3|.
A. 2.
B. 3.
C. 4.
D. 5.
- Câu 73 : Phần thực và phần ảo của số phức z thỏa mãn: (1 + i)2(2 - i) z = 8 + i + (1 + 2i)z lần lượt là?
A. -3; -2
B. 2; 3
C. 2; -3
D. Đáp án khác.
- Câu 74 : Số phức z thỏa mãn phương trình có phần thực và phần ảo lần lượt là:
A: -2; 5
B. -2 và 3
C. 2 và -3
D. 3 và 5
- Câu 75 : Tìm phần thực của số phức , biết rằng
A. 3.
B. -2.
C. – 4.
D. 5.
- Câu 76 : Có bao nhiêu số phức z thỏa |z| = 2 và z3 là số thực là:
A. 5
B. 3
C. 4
D. 6
- Câu 77 : Xác định tập hợp các điểm trong mặt phẳng biểu diễn số phức z thoả điều kiện |z + 1 – 3i| ≤ 4.
A. Hình tròn tâm I(-1;3), bán kính r = 4.
B. Đường tròn tâm I(-1;3), bán kính r = 4.
C. Hình tròn tâm I(-1; -3), bán kính r = 4.
D. Đường tròn tâm I(1;3), bán kính r = 4.
- Câu 78 : Giá trị của i105+ i23+ i20- i34 là ?
A. 2.
B. -2.
C. 4.
D. -4.
- Câu 79 : Với mọi số ảo z, số z2 + |z|2 là :
A. Số thực âm
B. Số 0
C. Số thực dương
D. Số ảo khác 0
- Câu 80 : Cho số phức z thỏa mãn: . Môđun của số phức z là
A. – 73.
B.
C. 73.
D.
- Câu 81 : Tìm số phức z , biết
A.z = -2 + i.
B. z = -2 - i.
C. z = 3 + 2i.
D. z = 2 - i.
- Câu 82 : Có bao nhiêu số phức z thỏa mãn và z2 là số thuần ảo ?
A. 4.
B. 3.
C. 2.
D. 1.
- Câu 83 : Tìm tất cả số phức z thỏa
A.
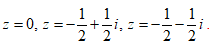
B.
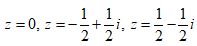
C.
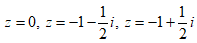
D.
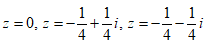
- Câu 84 : Số phức z thỏa mãn: là
A. 2 + i
B. -2 - i
C. -4 + i
D. 2 - i
- Câu 85 : Tìm số phức z thỏa mãn hệ thức và
A. z = 3 + 4i; z = 5.
B. z = 3 + 4i; z = -4.
C. z = -3 + 4i; z = 5.
D. z = 3 - 4i; z = -5.
- Câu 86 : Tìm số thực x; y để hai số phức z1 = 9y2 – 4 – 10xi5 và z2 = 8y2 + 20i11 là liên hợp của nhau?
A. x = -2; y = 2.
B. x = 2; y = ±2.
C. x = 2; y = 2.
D. x = -2; y = ±2.
- Câu 87 : Cho số phức z thỏa mãn z2 - 6z + 13 = 0 . Giá trị của là:
A.
B.
C.
D.
- Câu 88 : Cho số phức z thỏa . Viết z dưới dạng z = a + bi. Khi đó tổng a + b có giá trị bằng bao nhiêu?
A. 3.
B. -1.
C. 1.
D. 2.
- Câu 89 : Có bao nhiêu số phức z thỏa mãn: và
A. 2.
B. 3.
C. 0.
D. 1.
- Câu 90 : Tìm số phức z để
A. z = 0; z = 1 - i.
B. z = 0; z = 1 + i.
C. z = 0; z = 1 + i; z = 1 - i.
D. z = 1+ i; z = 1- i.
- Câu 91 : Tìm số nguyên x, y sao cho số phức z = x + yi thỏa mãn z3 = 18 + 26i
A.
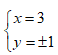
B.
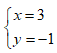
C.
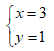
D.
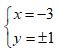
- Câu 92 : Cho số phức z = 3+ i. Điểm biểu diễn số phức 1/z trong mặt phẳng phức là:
A.
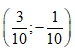
B.
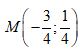
C.
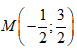
D.
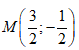
- Câu 93 : Căn bậc hai của số phức z = -3 + 4i có kết quả:
A. 1 + 2i.
B. 1 - 2i.
C. 1 + 3i.
D. Tất cả sai.
- Câu 94 : Tính căn bậc hai của số phức z = 8 + 6i ra kết quả:
A.
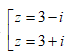
B.
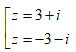
C.
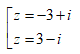
D.
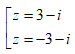
- Câu 95 : Cho z = 3 + 4i. Tìm căn bậc hai của z.
A. -2 + i và 2 - i
B. 2 + i và 2 - i
C. 2 + i và -2 - i
D. 3 - 2i và 2 - 3i
- Câu 96 : Gọi z là căn bậc hai có phần ảo âm của 33 - 56i. Phần thực của z là:
A. 6.
B. 7.
C. 4.
D. –4.
- Câu 97 : Trong C , căn bậc hai của -121 là:
A. -11i.
B. 11i.
C. -11.
D.11i và -11i.
- Câu 98 : Trong C, phương trình z2 + 3iz + 4 = 0 có nghiệm là:
A.
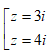
B.
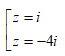
C.
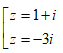
D.
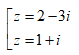
- Câu 99 : Cho z = 1 - i. Tìm căn bậc hai dạng lượng giác của z:
A.
B.
C.
D.
- Câu 100 : Trong C, phương trình (z2 + i) (z2 – 2iz – 1) = 0 có nghiệm là:
A.
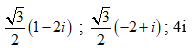
B. 1 - i; -1+ i; 2i
C.
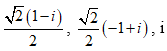
D. 1 - 2i; -15i; 3i
- Câu 101 : Trong C, phương trình có nghiệm là:
A.
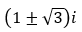
B.
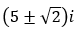
C.
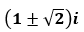
D.
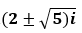
- Câu 102 : Trong C, phương trình 2x2 + x + 1 = 0 có nghiệm là:
A.
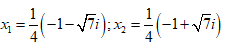
B.
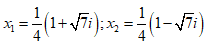
C.
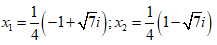
D.
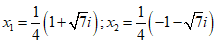
- Câu 103 : Trong C, phương trình z2 - z + 1 = 0 có nghiệm là:
A.
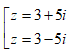
B.
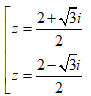
C.
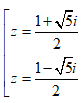
D.
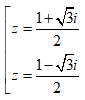
- Câu 104 : Gọi z1; z2 là hai nghiệm phức của phương trình z2 - 4z + 9 = 0; gọi M và N lần lượt là các điểm biểu diễn z1; z2 trên mặt phẳng phức. Tính độ dài đoạn thẳng MN.
A. 1
B. 2
C.
D.
- Câu 105 : Tìm các số thực b,c để phương trình z2 + bz + c = 0 nhận z = 1+ i làm một nghiệm.
A. b = -2; c = 3
B. b = -1; c = 2
C. b = -2; c = 2
D. b = 2; c = 2
- Câu 106 : Viết số phức sau dưới dạng lượng giác:
A.
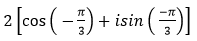
B.
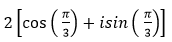
C.
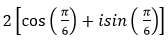
D.

- Câu 107 : Viết số phức sau dưới dạng lượng giác:
A.
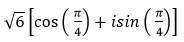
B.
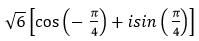
C.
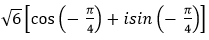
D.
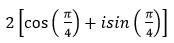
- Câu 108 : Viết số phức sau dưới dạng lượng giác: (1 + 3i)( 1 + 2i)
A.
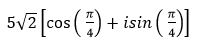
B.
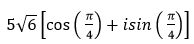
C.
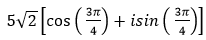
D.
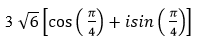
- Câu 109 : Viết số phức sau dưới dạng lượng giác:
A.
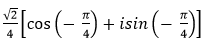
B.
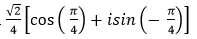
C.
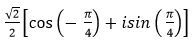
D.
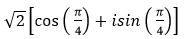
- Câu 110 : Viết số phức sau dưới dạng lượng giác:
A.
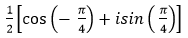
B.
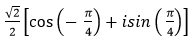
C.
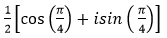
D.
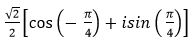
- Câu 111 : Viết số phức sau dưới dạng lượng giác
A.
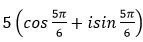
B.
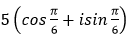
C.
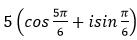
D.
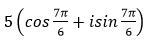
- Câu 112 : Tính giá trị của số phức sau
A. 1.
B. -1.
C. i.
D. -i.
- Câu 113 : Tính giá trị của số phức sau:
A.
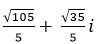
B.
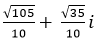
C.
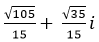
D. Tất cả sai.
- Câu 114 : Giá trị biểu thức sau: có phần thực là?
A. -1.
B. 0.
C.1.
D. 3.
- Câu 115 : Cho .Tính A= z12 + z6 + 1
A. 1.
B. 2.
C. 3.
D. 4.
- Câu 116 : Cho .Tính B = z9 + z6 + z3 + 1.
A. -2.
B. -1.
C. 0.
D. 1.
- Câu 117 : Trong C, nghiệm của phương trình z2 = -5 + 12i là:
A.
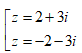
B. z = 2 + 3i
C. z = 2 - 3i
D.
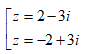
- Câu 118 : Trong C, phương trình z4 – 6z2 + 25 = 0 có nghiệm là:
A. ±8; ± 5i
B. ±3; ± 4i
C. ±5; ± 2i
D. ±(2 + i); ± (2 – i)
- Câu 119 : Biết z1 , z2 là hai nghiệm của phương trình 2. Khi đó giá trị của là:
A. 9/4.
B. 9.
C. 4.
D. -9/4.
- Câu 120 : Gọi z1 ; z2 là hai nghiệm phức của phương trình z2 - 4z+ 5= 0. Khi đó phần thực của là:
A. 5.
B. 6.
C. 4.
D.7.
- Câu 121 : Cho số phức z thỏa mãn z2 - 6z + 13 = 0. Tính
A.
B.
C.
D.
- Câu 122 : Trong C, phương trình |z| + z = 2 + 4i có nghiệm là:
A. z = -3 + 4i
B. z = -2 + 4i
C. z = -4 +4i
D. z = -5 + 4i
- Câu 123 : Trong C, nghiệm của phương trình z2 - 2z + 1 - 2i = 0 là
A.

B.
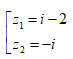
C.
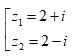
D.
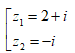
- Câu 124 : Trong C, phương trình z3 + 1= 0 có nghiệm là:
A.
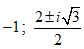
B.
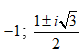
C.
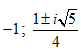
D.
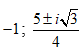
- Câu 125 : Trong C, phương trình z4 – 1 = 0 có nghiệm là:
A. ± 1; ± 2i
B. ± 2; ± 2i
C. ± 3; ± 4i
D. ± 1; ± i
- Câu 126 : Phương trình z3 = 8 có bao nhiêu nghiệm phức với phần ảo âm?
A. 1.
B. 2.
C. 3.
D. 0.
- Câu 127 : Trong C, phương trình z4 + 4= 0 có nghiệm là:
A. ±(1 - 4i) ; ±(1 + 4i)
B. ±(1 - 2i) ; ±(1 + 2i)
C. ±(1 - 3i) ; ±(1 +3i)
D. ±(1 - i) ; ±(1 + i)
- Câu 128 : Tập nghiệm trong C của phương trình z3 + z2 + z + 1 = 0 là:
A.{-1; -i ; i}
B.{-1 ; 1 ; i}
C. -1 ; i
D. 1 ; -1 ; i ; -i
- Câu 129 : Phương trình (2 + i) z2 + az + b = 0 có hai nghiệm là 3 + i và 1 - 2i. Khi đó a = ?
A. -9 - 2i.
B. 15 + 5i.
C. 9 + 2i.
D. 15 - 5i.
- Câu 130 : Giá trị của các số thực b ; c để phương trình z2 + bz + c = 0 nhận số phức z =1 + i làm một nghiệm là:
A.
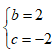
B.
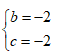
C.
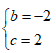
D.
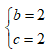
- Câu 131 : Trên tập hợp số phức, phương trình z2 + 7z + 15 = 0 có hai nghiệm . Giá trị biểu thức z1 + z2 + z1z2
A. –7
B. 8
C. 15
D. 22
- Câu 132 : Trên tập số phức, cho phương trình sau : ( z + i)4 + 4z2 = 0. Có bao nhiêu nhận xét đúng trong số các nhận xét sau?
A. 0.
B. 1.
C. 3.
D. 2.
- Câu 133 : Giả sử z1 , z2 là hai nghiệm của phương trình z2 - 2z + 5 = 0 và A, B là các điểm biểu diễn của z1 , z2 . Tọa độ trung điểm I của đoạn thẳng AB là:
A. I(1;1)
B. I(-1;0)
C. I(0;1)
D. I(1;0)
- Câu 134 : Cho hai số phức z = a + bi và z’ = a’ + b’i . Tìm điều kiện giữa a; b; a’; b’ để z + z’ là một số thuần ảo.
- - Trắc nghiệm Toán 12 Chương 2 Bài 1 Lũy thừa
- - Trắc nghiệm Toán 12 Chương 2 Bài 2 Hàm số lũy thừa
- - Trắc nghiệm Toán 12 Chương 2 Bài 4 Hàm số mũ và hàm số lôgarit
- - Trắc nghiệm Toán 12 Chương 2 Bài 5 Phương trình mũ và phương trình lôgarit
- - Trắc nghiệm Toán 12 Chương 2 Bài 6 Bất phương trình mũ và bất phương trình lôgarit
- - Trắc nghiệm Toán 12 Chương 3 Bài 1 Nguyên hàm
- - Trắc nghiệm Toán 12 Chương 3 Bài 2 Tích phân
- - Trắc nghiệm Toán 12 Chương 3 Bài 3 Ứng dụng của tích phân trong hình học
- - Trắc nghiệm Toán 12 Bài 1 Số phức
- - Trắc nghiệm Toán 12 Bài 2 Cộng, trừ và nhân số phức

