Giải bài 3 trang 67 - Sách giáo khoa Toán 8 tập 1

Đề bài

 Ta gọi tứ giác ABCD trên hình 8 có AB = AD, CB = CD là hình "cái diều".

a) Chứng minh rằng AC là đường trung trực của BD.

b) Tính $\widehat{B}, \widehat{D}$ biết rằng $\widehat{A}$$=100^0, \widehat{C} = 60^0$

Hướng dẫn giải

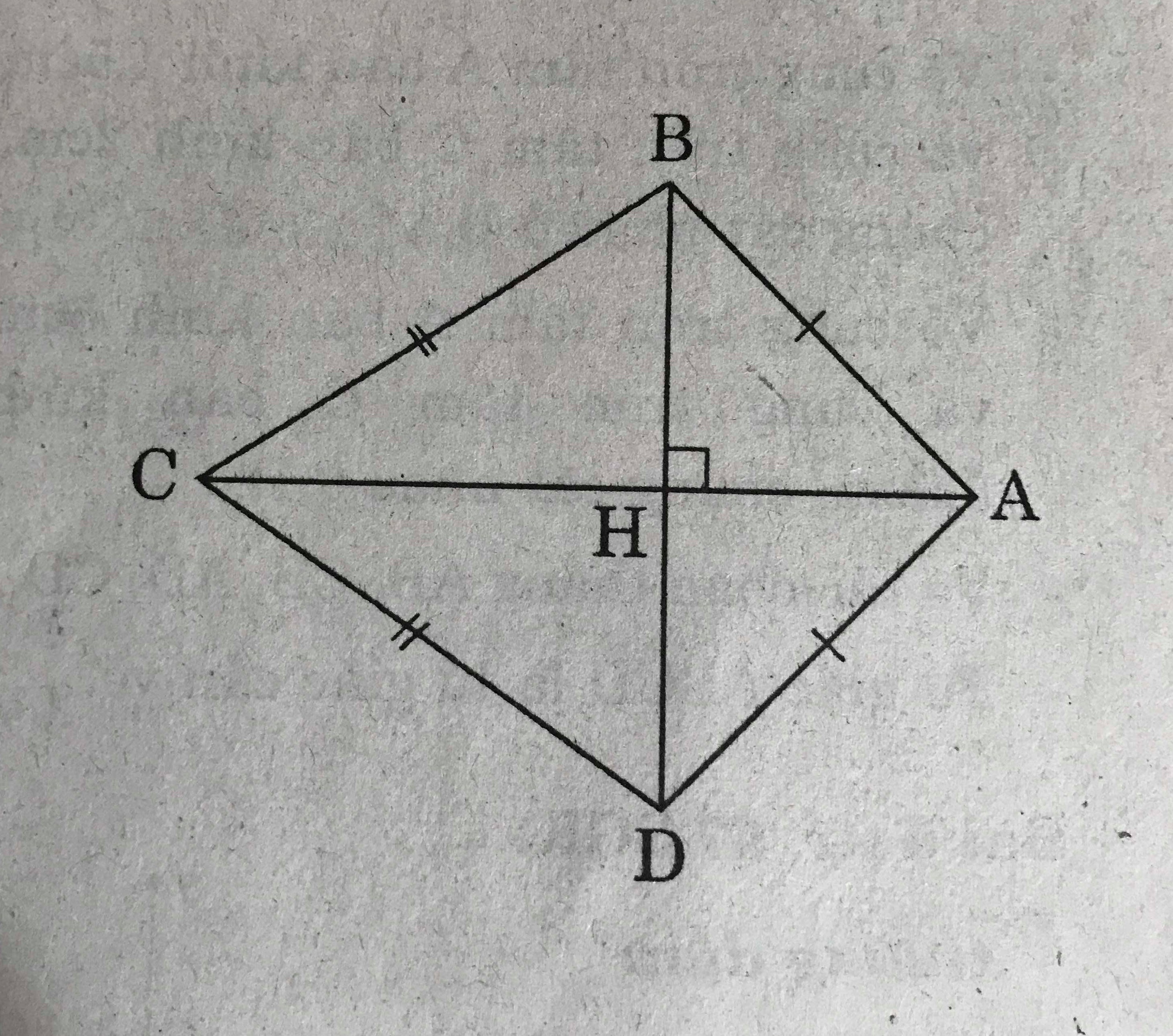
a) Kẻ AH $\perp$ BD

$\triangle$BAD có AB = AD nên là tam giác cân => AH là đường trung trực của BD    (1)

=> H là trung điểm của BD

$\triangle$BCD có CB = CD nên là tam giác cân => CH là đường trung trực của BD    (2)

Từ (1) và (2) suy ra AC là đường trung trực của BD.

b) Xét $\triangle$ABC và $\triangle$ADC có :

AB = AD (gt), CB = CD (gt), AC là cạnh chung.

Do đó : $\triangle$ABC = $\triangle$ADC (c.c.c)

=> $\widehat{ABC}=\widehat{ADC}$

Tứ giác ABCD có :

$\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0$

Do đó :

$100^0+\widehat{B}+60^0+\widehat{B}=360^0$

$2\widehat{B}+160^0 = 360^0$

$2\widehat{B}=200^0$

=> $\widehat{B}=100^0$

Nên $\widehat{D}=\widehat{B}=100^0$