Bài 55 trang 96 SGK Toán 8 tập 1

Đề bài

Cho hình bình hành $ABCD$, $O$ là giao điểm của hai đường chéo. Một đường thẳng đi qua $O$ cắt các cạnh $AB$ và $CD$ theo thứ tự ở $M$ và $N$. Chứng minh rằng điểm $M$ đối xứng với điểm $N$ qua $O$.

Hướng dẫn giải

Áp dụng: +) Tính chất hình bình hành.

+) Tính chất hai điểm đối xứng qua 1 điểm.

Lời giải chi tiết

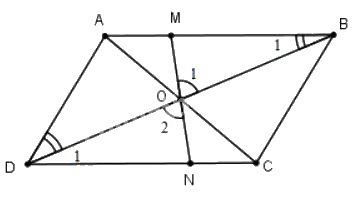
Vì $ABCD$ là hình bình hành (gt)

$\Rightarrow AB//DC$ (tính chất hình bình hành)

$\Rightarrow$ $\widehat{B_{1}}$ = $\widehat{D_{1}}$ (so le trong)

Xét $\Delta BOM$ và $\Delta DON$ có:

 $\widehat{B_{1}}$ = $\widehat{D_{1}}$ (cmt)

 $BO = DO$ (tính chất hình bình hành)

 $\widehat{O_{1}}$ = $\widehat{O_{2}}$ (đối đỉnh) 

$\Rightarrow$ $∆BOM = ∆DON (g.c.g)$

$\Rightarrow$ $OM = ON$ (hai cạnh tương ứng).

$\Rightarrow$ $O$ là trung điểm của $MN$ (dấu hiệu nhận biết trung điểm)

$\Rightarrow$ $M$ đối xứng với $N$ qua $O$.