Đề kiểm tra 15 phút - Đề số 2 - Bài 7, 8 - Chương 2 - Hình học 7

Đề bài

Bài 1. Cho tam giác nhọn ABC, kẻ AH vuông góc với BC $\left( {H \in BC} \right)$, biết $\Rightarrow AC = \sqrt {400}  = 20\,(cm)$ $AB = 13cm;\,AH = 12cm;\,$$HC = 16cm$. Tính AC, BC.

Bài 2. Cho tam giác ABC vuông tại A. Một đường thẳng cắt hai cạnh AB, AC ở D và E. Chứng minh: $C{D^2} - C{B^2} = E{D^2} - E{B^2}.$

Hướng dẫn giải

Bài 1.

Ta có $AH \bot BC$(giả thiết) nên $\Delta AHC$ vuông tại H.

Khi đó $A{C^2} = A{H^2} + C{H^2}$(định lí Pytago)

$= {12^2} + {16^2} = 400$

$\Rightarrow AC = \sqrt {400}  = 20\,(cm)$

Tương tự ta xét tam giác vuông AHB ta có

$\Rightarrow C{D^2} - C{B^2} = E{D^2} - E{B^2}.$ $B{H^2} = A{B^2} - A{H^2}$

$\Rightarrow BH = \sqrt {25}  = 5$(cm)$= {13^2} - {12^2} = 25$.

Vậy $BC = BH + HC = 5 + 16 = 21$(cm)

Bài 2.

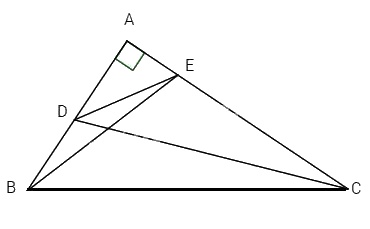
Nối C với D, E với B. Xét tam giác vuông CAD và ABC ta có

$\eqalign{  & C{D^2} = D{A^2} + C{A^2}  \cr  & C{B^2} = B{A^2} + C{A^2} \cr}$

$\Rightarrow C{D^2} - {\bf{C}}{B^2} = D{A^2} - B{A^2}$  (1)

Tương tạ xét tam giác vuông ADE và ABE $\eqalign{  & E{D^2} = D{A^2} + A{E^2}  \cr  & E{B^2} = A{E^2} + A{B^2} \cr}$

$\Rightarrow E{D^2} - E{B^2} = D{A^2} - B{A^2}$   (2)

Từ (1) và (2) $\Rightarrow C{D^2} - C{B^2} = E{D^2} - E{B^2}.$