Bài 27 trang 67 SGK Toán 7 tập 2

Đề bài

Hãy chứng minh định lí đảo của định lí trên : Nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.

Hướng dẫn giải

Ta sẽ chứng minh góc B = góc C hoặc AB = AC.

Lời giải chi tiết

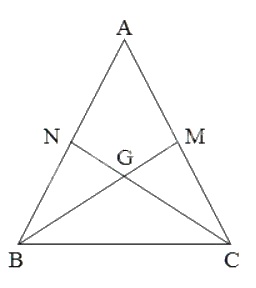
Giả sử ∆ABC có hai đường trung tuyến BM và CN cắt nhau ở G.

\(\Rightarrow \) G là trọng tâm của tam giác 

\(\Rightarrow \) GB = \(\frac{2}{3}\)BM; GC = \(\frac{2}{3}\)CN 

Mà BM = CN (giả thiết) nên GB = GC.

Tam giác GBC có GB = GC nên ∆GBC cân tại G

\(\Rightarrow \) \(\widehat{GCB} = \widehat{GBC}\)

Xét ∆BCN và ∆CBM có: 

BC là cạnh chung

CN = BM (gt)

\(\widehat{GCB} = \widehat{GBC}\) (cmt)

 Vậy ∆BCN = ∆CBM (c.g.c)

 \(\Rightarrow \)\(\widehat{NBC} = \widehat{MCB}\) 

\(\Rightarrow \)  ∆ABC cân tại A (đpcm).