Bài 13 trang 72 SGK Toán 9 tập 2

Đề bài

 Chứng minh rằng trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.

Hướng dẫn giải

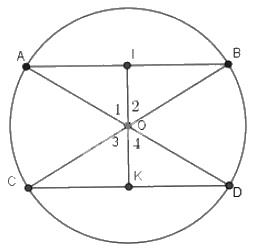
Giả sử \(AB\) và \(CD\) là các dây song song của đường tròn \((O)\).

Kẻ \(OI \bot AB\) \((I \in AB)\) và \(OK \bot CD (K\in CD)\).

Do \(AB //CD\) nên \(I,O,K\) thẳng hàng.

Do các tam giác \(OAB, OCD\) là các tam giác cân đỉnh \(O\) nên các đường cao kẻ từ đỉnh đồng thời là phân giác.

Vì vậy ta có: \(\widehat {{O_1}} = \widehat {{O_2}} = \widehat {{O_3}} = \widehat {{O_4}}\)

Giả sử \(AB\) nằm ngoài \(\widehat{COD}\), ta có: \(\widehat {AOC} = {180^0} - \widehat {{O_1}} - \widehat {{O_3}} = {180^0} - \widehat {{O_2}} - \widehat {{O_4}} = \widehat {BOD}\)

Suy ra  \(\overparen{AC}\)= \(\overparen{BD}\).