Đề kiểm tra 15 phút - Đề số 8 - Bài 1 - Chương 1 - Hình học 9

Đề bài

Cho ∆ABC vuông tại A. Đường phân giác AD chia cạnh BC thành hai đoạn \(BD = 36cm\) và \(CD = 60cm\). Kẻ đường cao AH của tam giác .

a. Tính tỉ số \({{HB} \over {HC}}\)

b. Tính chiều cao AH.

Hướng dẫn giải

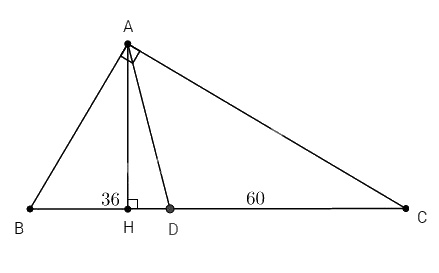
a. Ta có: AD là phân giác của ∆ABC nên:

\({{AB} \over {AC}} = {{DB} \over {DC}} = {{36} \over {60}} = {3 \over 5} \Rightarrow {{A{B^2}} \over {A{C^2}}} = {9 \over {25}}\)

Lại có: ∆ABC vuông tại A, đường cao AH nên:

\(A{B^2} = BC.HB\) (định lí 1)

\(A{C^2} = BC.HC\) (định lí 1)

\( \Rightarrow {{HB} \over {HC}} = {{A{B^2}} \over {A{C^2}}} = {9 \over {25}}\)

b. Ta có: \({{HB} \over {HC}} = {9 \over {25}}\) (cmt)

\( \Rightarrow {{HB} \over 9} = {{HC} \over {25}} = {{HB + HC} \over {9 + 25}} = {{BD + DC} \over {9 + 25}}\)

\(= {{36 + 60} \over {34}} = {{96} \over {34}} = {{48} \over {17}}\)

Do đó: \(HB = {{48.9} \over {17}} \approx 25,4\,\left( {cm} \right)\)

\( \Rightarrow HC = 96 - 25,4 \approx 70,6\,\left( {cm} \right)\)

Vậy \(A{H^2} = HB.HC\) (định lí 2)

\( \Rightarrow AH = \sqrt {HB.HC} \)\(\; \approx \sqrt {25,4.70,6}  \approx 42\,\left( {cm} \right)\)