Bài 7 trang 56 SGK Toán 7 tập 2
Đề bài
Cho tam giác ΔABCΔABC với AC>ABAC>AB. Trên tia ACAC, lấy điểm B′ sao cho AB′=AB
a) Hãy so sánh góc ^ABC với góc ^ABB′
b) Hãy so sánh góc ^ABB′ với góc ^AB′B
c) Hãy so sánh góc ^AB′B với góc ^ACB
Từ đó suy ra ^ABC>^ACB
Hướng dẫn giải
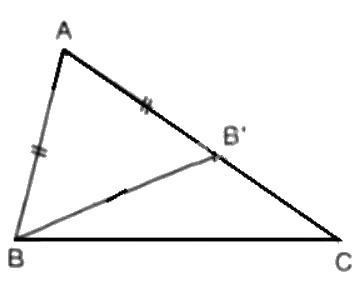
a) Trên tia AC, AB′=AB
Mà \(AB
Nên B′ nằm giữa A và C
=> tia BB′ nằm giữa hai tia BA và BC
=>^ABB′<^abc
b) ∆ABB' có AB=AB′ nên cân tại A
=>^ABB′=^AB′B
c) Vì góc ^AB′B là góc ngoài tại B′ của ΔBB′C nên
^AB′B=^B′BC+^B′CB
Mà ^B′CB=^ACB
Do đó: ^AB′B>^ACB (1)
Mặt khác: ^ABB′=^AB′B ( theo b) (2)
^ABB′<^abc (câu a) (3)
Từ (1), (2) và (3) suy ra: ^ABC>^ACB
Liên kết với Facebook
Liên kết với Google