Cho hàm số
Câu hỏi: Cho hàm số 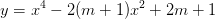 có đồ thị là (Cm).
có đồ thị là (Cm).
A m = 3 và m = 1/6
B m = 1 và m = 0
C m = 4 và m = -4/9
D m = 0
Câu hỏi trên thuộc đề trắc nghiệm
- Sự tương giao của hàm bậc 4, hàm bậc nhất trên bậc nhất - Có video chữa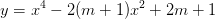 có đồ thị là (Cm).
có đồ thị là (Cm). A m = 3 và m = 1/6
B m = 1 và m = 0
C m = 4 và m = -4/9
D m = 0
Đáp án
C
- Hướng dẫn giải
Phương pháp giải:
Giải chi tiết:
1.Với m = 0, y = x4 – 2x2 + 1
- Tập xác định D = R. (0,25)
- Sự biến thiên :
+ Giới hạn của hàm số tại vô cực :
![]() (0,25)
(0,25)
![]() (0,25)
(0,25)
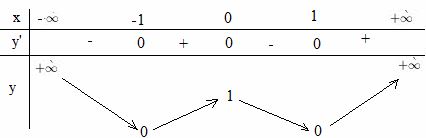
+ Bảng biến thiên :
y’ = 4x3 - 4x
y’ = 0 <=> 4x(x2 – 1) = 0
⇔ 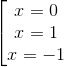 (0,25)
(0,25)
 (0,25)
(0,25)
Hàm số đồng biến trên mỗi khoảng (-1 ; 0) và (1 ; +∞).
Hàm số nghịch biến trên mỗi khoảng (-∞ ; -1) và (0 ; 1) (0,25)
Hàm số đạt cực đại tại x = 0, yCĐ = 1
Hàm số đạt cực tiểu tại x = ± 1 và yCT = 0 (0,25)
- Đồ thị
Cho x = 0 => y = 1
CHo y = 0, x = ±1
Đồ thị nhận Oy làm trục đối xứng.
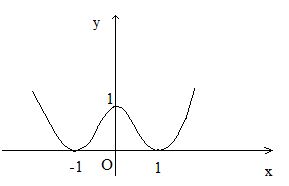 (0,25)
(0,25)
2.Phương trình hoành độ giao điểm :
x4 – 2(m + 1) x2 + 2m + 1 = 0 (1)
Đặt t = x2 (t ≥ 0)
(1) ⇔ t2 – 2(m + 1)t + 2m + 1 = 0 (2) (0,25)
Để (Cm) cắt Ox tại 4 điểm phân biệt ⇔ Phương trình (1) có 4 nghiệm phân biệt ⇔ Phương trình (2) có hai nghiệm phân biệt 0 < t1 < t2. (0,25)
⇔ 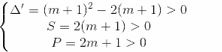 (0,25)
(0,25)
⇔ 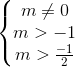
⇔ 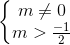 (0,25)
(0,25)
Hoành độ của 4 giao điểm là x = ± 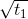 , x = ±
, x = ± 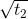
Sắp xếp theo chiều tăng dần : -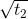 , -
, -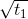 ;
; 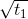 ;
; 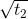
Do 4 hoành độ lập thành một cấp số cộng
=> 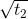 = 3.
= 3.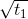 (0,25)
(0,25)
⇔ t2 = 9t1
Kết hợp hệ thức Vi-ét :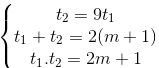 (0,25)
(0,25)
=> ![]() ;
; ![]() (0,25)
(0,25)
=> ![]()
⇔ 9m2 – 32m – 16 = 0
⇔ 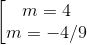 ( t/m). (0,25)
( t/m). (0,25)
Câu hỏi trên thuộc đề trắc nghiệm
- Sự tương giao của hàm bậc 4, hàm bậc nhất trên bậc nhất - Có video chữaEmail: [email protected]
Liên hệĐịa chỉ: 102, Thái Thịnh, Trung Liệt, Đống Đa, Hà Nội
Email: [email protected]
