Lý thuyết Góc ở tâm Số đo cung chi tiết nhất

Góc ở tâm. Số đo cung là một trong những phần kiến thức cơ bản nhất của chương III Hình học 9 nghiên cứu về Góc và đường tròn. Cunghocvui xin gửi tới các bạn bài giảng góc ở tâm số đo cung và các bài tập về góc ở tâm số đo cung đầy đủ và chi tiết nhất. Hy vọng với toán 9 góc ở tâm số đo cung sẽ hữu ích với các bạn!

A. Một số lý thuyết cần nhớ về góc ở tâm. Số đo cung

1. Các kiến thức về góc ở tâm. Số đo cung

- Trong phạm vi một đường tròn, đỉnh của một góc trùng với vị trí tâm của đường tròn thì góc đó được gọi là góc ở tâm. 

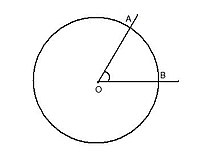
- Một số tính chất của góc ở tâm:

+ Nếu góc ở tâm lớn hơn \(0^0\) và nhỏ hơn \(180^0\) thì cung được bao bởi góc được gọi là cung nhỏ, cung lớn là cung nằm bên ngoài góc (cung lớn luôn có số đo lớn hơn \(180^0\))

+ Nếu góc ở tâm bằng đúng \(180^0\) thì góc đó chia đường tròn thành hai nửa đường tròn bằng nhau, mỗi nửa đường tròn là một cung.

+ Cung bị chắn là cung được bao bởi góc ở tâm. Nửa đường tròn được chắn bởi một góc bẹt.

2. Các kiến thức về số đo cung

- Số đo góc ở tâm chứa cung nhỏ cũng là số đo của cung nhỏ đó. 

- Số đo của một cung lớn có chung hai mút thuộc đường tròn với cung nhỏ được tính bằng công thức lấy hiệu của \(360^0\) trừ đi số đo của cung nhỏ.

- Số đo của cung nửa đường tròn bằng \(180^0\), \(0^0\) là số đo của cung không (cung đặc biệt có hai mút thuộc đường tròn trùng vị trí của nhau)

3. Các kiến thức cần nhớ khi so sánh hai cung trong một hoặc nhiều đường tròn bằng nhau 

Khi so sánh hai cung trong một hoặc nhiều đường tròn bằng nhau, ta có những tính chất sau:

- Nếu hai cung bằng nhau về số đo thì được gọi là hai cung bằng nhau.

- Trong hai cung cùng thuộc một đường tròn hoặc nhiều đường tròn bằng nhau thì cung nào lớn hơn về số đo thì cung đó được gọi là cung lớn hơn.

4. Định lý góc ở tâm số đo cung

Nếu trên một cung \(AB\) chứa một điểm C thì ta có:

\(sđ\overbrace{AB}\) = \(sđ\overbrace{AC}\) + \(sđ\overbrace{CB}\)

B. Các bài tập về góc ở tâm số đo cung

Bài 1: Tính số đo độ của góc ở tâm trong các trường hợp sau đây:

a, Khi kim đồng hồ dịch chuyển từ 1 giờ đến 3 giờ?

b, Khi kim đồng hồ dịch chuyển từ 3 giờ đến 6 giờ?

Trả lời: Khi kim đồng hồ dịch chuyển từ 1 giờ đến 3 giờ thì góc ở tâm có số đo là \(60^0\)

            Khi kim đồng hồ dịch chuyển từ 3 giờ đến 9 giờ thì góc ở tâm có số đo là \(90^0\)

Bài 2: Xuất phát từ điểm M không thuộc đường tròn tâm O với bán kính là R, kẻ hai tiếp tuyến \(MA\) và \(MB\) đến đường tròn (\(A, B\) là hai tiếp điểm thuộc đường tròn tâm O). Biết rằng độ dài khoảng cách của \(OM\) gấp đôi độ dài của bán kính, hỏi góc \(\widehat{AOB}\) có độ lớn là bao nhiêu?

Hướng dẫn giải: Vì tam giác \(OAM\) là một nửa của tam giác đều nên ta có \(\widehat{AOM}=60^0\)

Theo tính chất của hai tiếp tuyến cắt nhau của một đường tròn thì \(\widehat{AOB}=2.\widehat{AOM}\) 

=> \(\widehat{AOB}=2.60^0=120^0\)

Bài 3: Gọi hai điểm A và B là giao điểm cắt của hai đường tròn tâm O bán kính R và đường tròn tâm O' bán kính R'. Trong các trường hợp sau đây, hãy so sánh độ lớn của hai bán kính R và R':

a, Trong đường tròn tâm O bán kính R có số đo một cung nhỏ \(AB\) lớn hơn số đo một cung nhỏ \(AB\) của đường tròn tâm O' bán kính R'?

b,  Trong đường tròn tâm O bán kính R có số đo một cung nhỏ \(AB\) nhỏ hơn số đo một cung lớn \(AB\) của đường tròn tâm O' bán kính R'?

c,  Trong đường tròn tâm O bán kính R có số đo một cung nhỏ \(AB\) bằng số đo một cung nhỏ \(AB\) của đường tròn tâm O' bán kính R'?

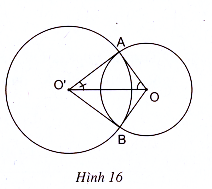
Hướng dẫn giải bài tập:

a, Vì theo giả thiết của đề bài trong đường tròn tâm O bán kính R có số đo một cung nhỏ \(AB\) lớn hơn số đo một cung nhỏ \(AB\) của đường tròn tâm O' bán kính R' => \(\widehat{AOB}>\widehat{AO'B}\) (theo tính chất của hai dây cung)

Xét trong tam giác \(AOO'\) có \(\widehat{AOO'}>\widehat{AO'O}\) (vì \(OO'\) là tia phân giác của hai góc ở tâm) 

=> \(O'A>OA\) hay nói cách khác là \(R'>R\)

b, Chứng minh tương tự như ý a (sử dụng lý thuyết tổng số đo của cung lớn và cung nhỏ cùng hai đầu mút trên một đường tròn luôn bằng \(360^0\) kết hợp với giả thiết đề bài là trong đường tròn tâm O bán kính R có số đo một cung nhỏ \(AB\) nhỏ hơn số đo một cung lớn \(AB\) của đường tròn tâm O' bán kính R')

c, Sử dụng cách tương tự để suy ra \(\Delta AOO'\) là một tam giác cân => \(O'A=OA\) hay \(R=R'\)

Bài 4: Trên đường tròn tâm O bán kính R lấy một điểm C bất kỳ nằm trên một cung nhỏ \(AB\). Điểm C bất kỳ đó chia cung lớn \(AB\) thành hai cung là \(AC\) và \(CB\). Hãy sáng tỏ rằng cung lớn \(AB\) có số đo cung bằng tổng số đo của hai cung \(AC\) và cung \(CB\)?

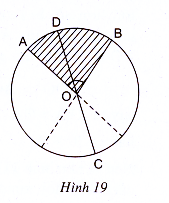
Để chứng minh rằng \(sđ\overbrace{AB}\) = \(sđ\overbrace{AC}\) + \(sđ\overbrace{CB}\) ta xét đến ba trường hợp như sau:

a, Trường hợp 1: Điểm C thuộc cung chắn góc đối đỉnh của \(\widehat{AOB}\)

Trong phạm vi đường tròn tâm O bán kính R, kẻ đường kính \(CD\)

Theo dữ kiện đề bài, ta có: 

\(\widehat{DOA}\) + \(\widehat{AOC}\) = \(180^0\)

\(\widehat{DOB}\) + \(\widehat{BOC}\) = \(180^0\)

=> \(\widehat{DOA}\) + \(\widehat{AOC}\) + \(\widehat{DOB}\) + \(\widehat{BOC}\) = \(360^0\) mà \(\widehat{DOA}\) + \(\widehat{DOB}\) = \(\widehat{AOB}\)

=> \(\widehat{AOB}\) + \(\widehat{DOB}\) + \(\widehat{BOC}\) = \(360^0\) (hay nói cách khác là tổng số đo của ba cung nhỏ là \(AB,AC,CB\) bằng \(360^0\)) 

Mặt khác số đo cung lớn \(AB\) = \(360^0\) - số đo cung nhỏ \(AB\)

=> Số đo cung lớn \(AB\) sẽ bằng tổng số đo hay cung nhỏ là cung \(AC\) và cung \(CB\)

Vậy  \(sđ\overbrace{AB}\) = \(sđ\overbrace{AC}\) + \(sđ\overbrace{CB}\) (điều phải chứng minh)

b, Trường hợp 2: Điểm C trùng với một trong hai điểm cắt của \(OA\) hoặc \(OB\)

Theo dữ kiện đề bài, ta có: 

\(\widehat{AOB}\) + \(\widehat{BOC}\) = \(180^0\)

\(\widehat{AOC}\) = \(180^0\)

=> \(\widehat{AOB}\) + \(\widehat{BOC}\) + \(\widehat{AOC}\) = \(360^0\) <=> \(\widehat{AOC}\) + \(\widehat{BOC}\) = \(360^0\) - \(\widehat{AOB}\)

Mặt khác số đo cung lớn \(AB\) = \(360^0\) - số đo cung nhỏ \(AB\)

=> Số đo cung lớn \(AB\) sẽ bằng tổng số đo hay cung nhỏ là cung \(AC\) và cung \(CB\)

Vậy  \(sđ\overbrace{AB}\) = \(sđ\overbrace{AC}\) + \(sđ\overbrace{CB}\) (điều phải chứng minh)

c, Trường hợp 3: Điểm C thuộc góc kề bù với góc ở tâm 

Theo ý b, ta có cung lớn \(AB\) được tính bằng công thức tổng của số đo cung nhỏ \(EB\) và nửa cung tròn \(AE\)

Khi điểm C thuộc vào cung nhỏ \(EB\) thì ta có cung nhỏ \(EB\) được tính bằng công thức tổng của số đo cung nhỏ \(EC\) và số đo cung nhỏ \(CB\) (\(sđ\overbrace{EB}\) = \(sđ\overbrace{EC}\) + \(sđ\overbrace{CB}\))

Số đo cung \(AE\) sẽ được tính bằng công thức hiệu của số đo cung lớn \(AC\) trừ đi số đo cung \(EC\)

Vậy số đo cung lớn \(AB\) được tính bằng công thức tổng số đo cung lớn \(AC\) và số đo cung nhỏ \(CB\) hay theo công thức là  \(sđ\overbrace{AB}\) = \(sđ\overbrace{AC}\) + \(sđ\overbrace{CB}\) (điều phải chứng minh)

Bài 5: Gọi hai điểm A và B là giao điểm cắt của hai đường tròn tâm O bán kính R và đường tròn tâm O' bán kính R'. Giao điểm cắt của hai đường tròn tâm O bán kính R và đường tròn tâm O' bán kính R' với đường phân giác của \(\widehat{OBO'}\) lần lượt tại hai điểm là C và D. Xét về yếu tố độ lớn của góc, hãy so sánh \(\widehat{BOC}\) và \(\widehat{BO'D}\)

Trả lời: \(\widehat{BOC}\) = \(\widehat{BO'D}\)

Bài 6: Cho một cung lớn AB có số đo bằng \(140^0\) của đường tròn tâm O bán kính R và B và A lần lượt là điểm chính giữa của cung AD và CB. Hỏi hai cung nhỏ CD và cung lớn CD có số đo bằng bao nhiêu?

Theo dữ kiện đề bài ta có \(\widehat{AOB}=140^0\) = \(\widehat{BOD}\) = \(\widehat{COA}\)

Qua tâm O của đường tròn đường kính R, kẻ hai đường kính là AA' và BB'. Ta có:

\(\widehat{AOB'}=180^0-\widehat{AOB}\) = \(180^0-140^0\) = \(40^0\)

=> \(\widehat{BOA'} =40^0\) (vì là hai góc đối đỉnh với \(\widehat{AOB'}\))

\(\widehat{B'OD}=180^0-\widehat{BOD}\) = \(180^0-140^0\) = \(40^0\)

=> \(\widehat{COD}=\widehat{COA}-\widehat{AOB'}-\widehat{B'OD}\) = \(140^0-40^0-40^0\) = \(60^0\)

Trả lời: Cung lớn CD có số đo là \(300^0\) và cung nhỏ CD có số đo là \(60^0\).

Tham khảo thêm >>> Giải bài tập sách giáo khoa bài Góc ở tâm. số đo cung Toán 9

Cunghocvui đã gửi đến các bạn bài lý thuyết góc ở tâm số đo cung và các các bài tập về góc ở tâm số đo cung qua bài giảng góc ở tâm số đo cung. Nếu có đóng góp hay thắc mắc gì cho bài viết toán 9 góc ở tâm số đo cung, các bạn hãy để lại comment xuống dưới phần bình luận nhé!