Giải bài 9 trang 135 - Sách giáo khoa Toán 9 tập 2

Đề bài

   Cho tam giác ABC nội tiếp đường tròn (O') và ngoại tiếp đường tròn (O). Tia AO cắt đường tròn (O') tại D. Ta có:

   (A) CD = BD = O'D ;    (B) AO = CO = OD

   (C) CD = CO = BD ;      (D) CD = OD = BD

   Hãy chọn câu trả lời đúng.

Hướng dẫn giải

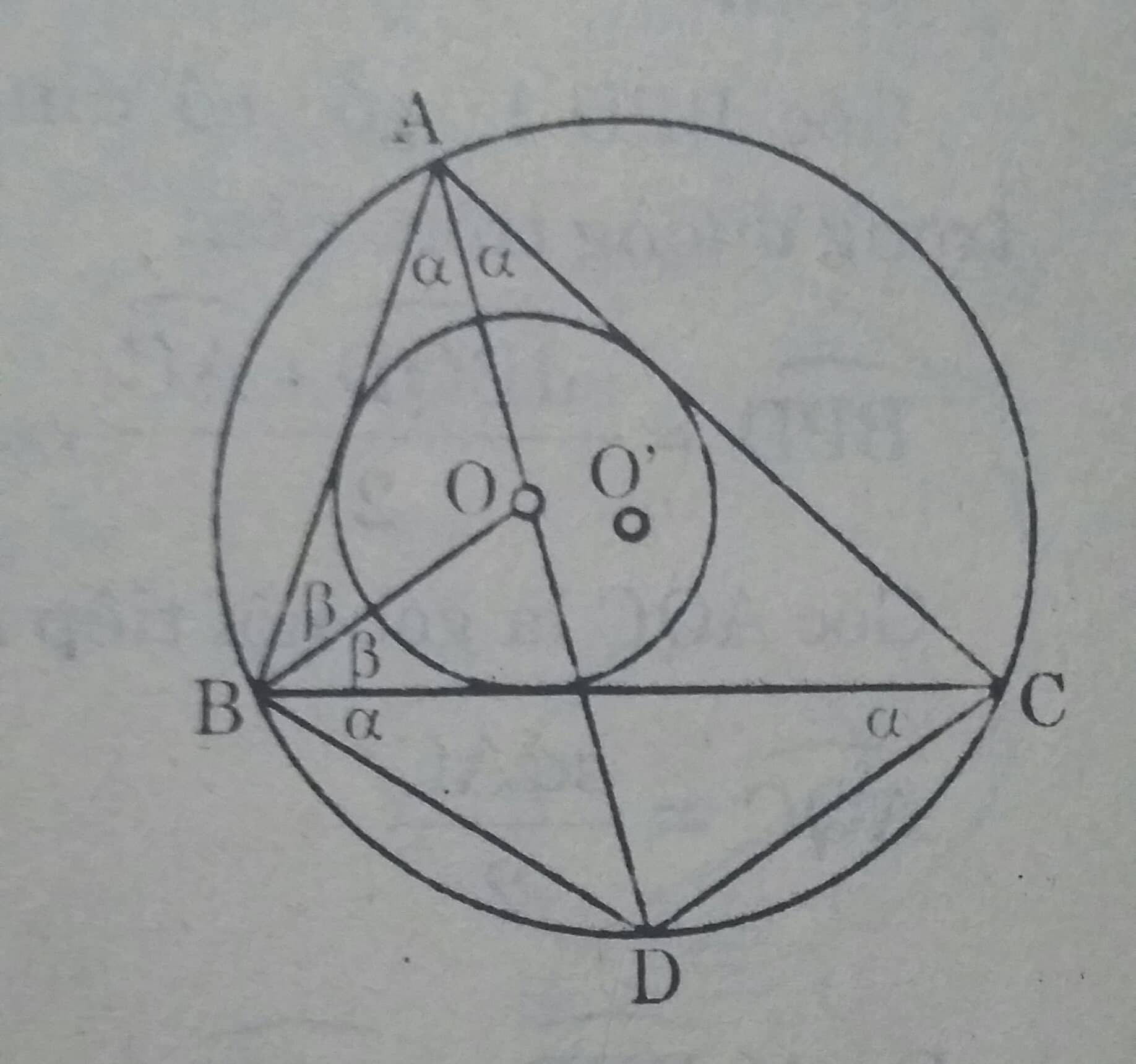
   Đường tròn (O) nội tiếp \(\Delta ABC \) nên theo tính chất hai tiếp tuyến cắt nhau ta được:

   \(\widehat{BAO}= \widehat{CAO}= \alpha\\\\widehat{ABO}=\widehat{CBO}= \beta\\ Suy \ ra \stackrel\frown{BD} = \stackrel\frown{DC} \ và \ DB = DC \\\)

   Ta lại có \(\widehat{BOD}= \alpha + \beta \) ( góc ngoài của tam giác AOB)

   Suy ra \(\widehat{BOD}= \widehat{OBD} \Rightarrow \Delta DOB \ cân \ ở \ D.\)

   Vậy DB = DO (2)

   Từ (1) và (2) suy ra DB = DC = DO 

   Chọn D.