Đề kiểm 15 phút - Đề số 7 - Bài 4 - Chương 3 - Hình học 9

Đề bài

Từ một điểm P ở ngoài đường tròn (O), kẻ hai tiếp tuyến PA, PB đến đường tròn. Trên cung nhỏ AB lấy điểm C bất kì, kẻ các đường vuông góc CD, CE, CF lần lượt xuống các đường thẳng AB, BP, PA. Chứng minh rằng : $\widehat {DCF} = \widehat {DCE}$ và $\widehat {DFC} = \widehat {CDE}$.

Hướng dẫn giải

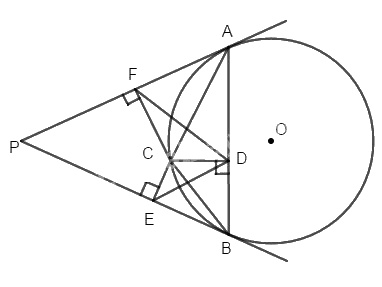
Ta có E và D nằm trên đường tròn đường kính BC, F và D nằm trên đường tròn đường kính AC.

Do đó $\widehat {DCF} + \widehat {PAB} = \widehat {DCE} + \widehat {PBA} = 2v$

Trong đó $\widehat {PAB} = \widehat {PBA}$ ( góc giữa tiếp tuyến và một dây cùng chắn cung nhỏ AB).

Vậy $\widehat {DCF} = \widehat {DCE}$.

Trong đường tròn (O), ta có : $\widehat {CBE} = \widehat {CAB}$ (góc giữa tiếp tuyến và một dây và góc nội tiếp cùng chắn cung CB).

Trong đường tròn đường kính BC, ta có : $\widehat {CBE} = \widehat {CDE}$ ( góc nội tiếp cùng chắn cung CE).

Trong đường tròn đường kính CA, ta có : $\widehat {CAB} = \widehat {DFC}$ ( góc nội tiếp cùng chắn cung CD).

Vậy $\widehat {DFC} = \widehat {CDE}$.