Bài 5 trang 121 SGK Hình học 11

Đề bài

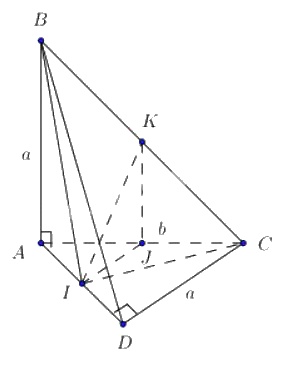
Tứ diện \(ABCD\) có hai mặt \(ABC\) và \(ADC\) nằm trong hai mặt phẳng vuông góc với nhau. Tam giác \(ABC\) vuông tại \(A\) có \(AB = a, AC = b\). Tam giác \(ADC\) vuông tại \(D\) có \(CD = a\).

a) Chứng minh các tam giác \(BAD\) và \(BDC\) đều là tam giác vuông

b) Gọi \(I\) và \(K\) lần lượt là trung điểm của \(AD\) và \(BC\). Chứng minh \(IK\) là đoạn vuông góc chung của hai đường thẳng \(AD\) và \(BC\).

Hướng dẫn giải

a) Chứng minh \(BA \bot \left( {ACD} \right);\,\,CD \bot \left( {ABD} \right)\).

b) Gọi J là trung điểm của BC, chứng minh \(AD \bot \left( {IJK} \right) \Rightarrow IK \bot AD\).

Chứng minh tam giác \(IBC\) cân tại I \( \Rightarrow IK \bot BC\).

Lời giải chi tiết

a) 

\(\left\{ \begin{array}{l}
\left( {ABC} \right) \bot \left( {ADC} \right)\\
\left( {ABC} \right) \cap \left( {ADC} \right) = AC\\
\left( {ABC} \right) \supset AB \bot AC
\end{array} \right. \Rightarrow BA \bot \left( {ADC} \right)\)

\( \Rightarrow BA \bot AD \Rightarrow \Delta BAD\) vuông tại A.

\(\left\{ \begin{array}{l}
BA \bot \left( {ADC} \right) \Rightarrow CD \bot BA\\
CD \bot AD
\end{array} \right. \Rightarrow CD \bot \left( {BAD} \right)\)

\( \Rightarrow CD \bot DB \Rightarrow \Delta BDC\) vuông tại D.

b) Gọi \(J\) là trung điểm của \(AC\Rightarrow KJ//BA\)

Mà \(BA⊥(ADC) ⇒ KJ ⊥(ADC)⇒ KJ ⊥ AD\)      (1)

Ta cũng có \(IJ//DC ⇒ IJ ⊥ AD\)                                    (2)

Từ (1) và (2) suy ra: \(AD⊥(KIJ)⇒ AD ⊥ IK\,\,\,(3)\)

Ta lại có: \(ΔBAI = ΔCDI  (c.g.c)⇒ IB = IC\)

\(⇒ ΔBIC\) cân đỉnh \(I ⇒ IK ⊥ BC\)   (4)

Từ (3) và (4) suy ra \(IK\) là đoạn vuông góc chung của \(AD\) và \(BC\).