Bài 5 trang 119 SGK Hình học 11

Đề bài

Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(a\).

a) Chứng minh rằng \(B'D\) vuông góc với mặt phẳng \((BA'C')\).

b) Tính khoảng cách giữa hai mặt phẳng \((BA'C')\) và \((ACD')\).

c) Tính khoảng cách giữa hai đường thẳng \(BC'\) và \(CD'\).

Hướng dẫn giải

a) Một điểm cách đều ba điểm của một mặt phẳng thì thuộc trục của mặt phẳng đó (Trục của đường thẳng là đường thẳng đi qua tâm đường tròn ngoại tiếp và vuông góc với mặt phẳng đó).

Chứng minh B'D là trục của mặt phẳng \((BA'C')\).

b) Chứng minh tương tự ta được \(B'D\bot (ACD')\), từ đó suy ra \((BA'C') // (ACD')\). Xác định khoảng cách giữa hai mặt phẳng song song.

c) Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó.

Lời giải chi tiết

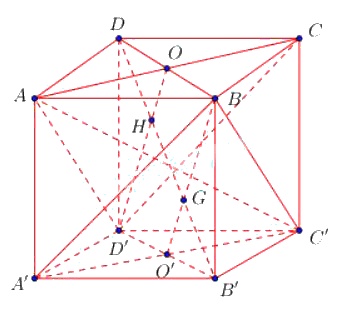
a) Ta có \(B'A' = B'B = B'C'\)

\( \Rightarrow B'\) thuộc trục của tam giác \(A'BC'\)            (1)

\(DA' = DB = DC'\) (đường chéo các hình vuông bằng nhau)

\(\Rightarrow D\) cũng thuộc trục của tam giác \(A'BC' \)    (2)

Từ (1) và (2) \(\Rightarrow B'D\) là trục của \((BA'C')\) \( \Rightarrow \bot (BA'C')\). 

b) Chứng minh tương tự ta được \(B'D\bot (ACD')\)

\(\left\{ \begin{array}{l}B'D \bot \left( {BA'C'} \right)\\BD' \bot \left( {ACD'} \right)\end{array} \right. \Rightarrow \left( {BA'C'} \right)//\left( {ACD'} \right)\)

Gọi \(G = B'D \cap \left( {BA'C'} \right);\,\,H = B'D \cap \left( {ACD'} \right) \)

\(\Rightarrow d\left( {\left( {BA'C'} \right);\left( {ACD'} \right)} \right) = HK\)

Ta có:

\(O'G//D'H\), \(O'\) là trung điểm của \(B'D' \Rightarrow G\) là trung điểm của \(B'H\).

\( \Rightarrow GB'=GH\)  (3)

\(OH//GB\), \(O\) là trung điểm của \(BD \Rightarrow H\) là trung điểm của \(DG\).

\( \Rightarrow HG=HD\)  (4)

Từ (3) và (4) suy ra: \(GB' = GH = HD \Rightarrow GH = \frac{1}{3}B'D\)

Do \(ABCD.A'B'C'D'\) là hình lập phương cạnh \(a\)

\( \Rightarrow B'D = a\sqrt 3  \Rightarrow HG = \frac{{a\sqrt 3 }}{3}\).

Vậy \(d\left( {\left( {BA'C'} \right);\left( {ACD'} \right)} \right) = \frac{{a\sqrt 3 }}{3}\).

c) \(BC' ⊂ (BA'C')\); \(CD' ⊂ (ACD')\), mà \( \left( {BA'C'} \right)//\left( {ACD'} \right)\)

Vậy \(d(BC', CD') = d((BA'C'),(ACD'))= \frac{a\sqrt{3}}{3}.\)