Bài 3 trang 45 SGK Toán 9 tập 1

Đề bài

Cho hai hàm số \(y = 2x\) và \(y = -2x\).

a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đã cho.

b) Trong hai hàm số đã cho, hàm số nào đồng biến ? Hàm số nào nghịch biến ? Vì sao ?

Hướng dẫn giải

a) Cách vẽ đồ thị hàm số \(y=ax,\ (a \ne 0)\):  Cho \(x=x_0 \Rightarrow y_0=ax_0\)

Đồ thị hàm số \(y=ax\, \, (a\neq 0)\) là đường thẳng đi qua gốc tọa độ và điểm \(A(x_0;y_0)\)

b) Với \({x_1},{x_2} \in \mathbb{R}\):

Nếu \( x_1  < x_2\)  và   \(f(x_1) < f(x_2)\)  thì hàm số \(y=f(x)\) đồng biến trên \(\mathbb{R}\).

Nếu \( x_1  < x_2\)  và   \(f(x_1) > f(x_2)\)  thì hàm số \(y=f(x)\) nghịch biến trên \(\mathbb{R}\).

Lời giải chi tiết

a)

+) Hàm số:  \(y = 2x\)

Cho \(x=1 \Rightarrow y=2.1=2 \Rightarrow A(1; 2) \).

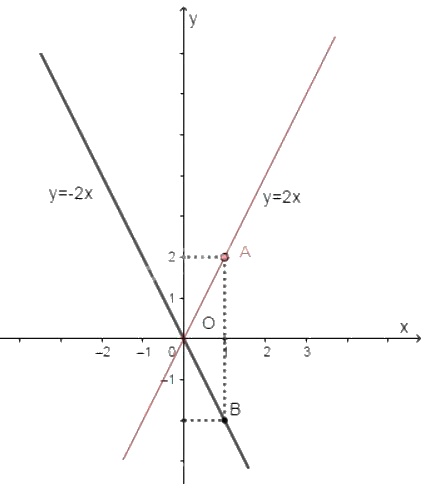
Đồ thị của hàm số \(y = 2x\) là đường thẳng đi qua \(O\) và điểm \(A(1; 2)\).

+) Hàm số:  \(y = -2x\)

Cho \(x=1 \Rightarrow y=-2.1=-2 \Rightarrow B(1; -2) \).

Đồ thị của hàm số \(y = -2x\) là đường thẳng đi qua \(O\) và điểm \(B(1; -2)\).

b) Cách 1:

+) Với mọi \(x_1, x_2 \in \mathbb{R}\) mà \(x_1 < x_2 \Rightarrow 2x_1 < 2x_2 \Rightarrow f(x_1) < f(x_2)\)

Do đó hàm số \(y = 2x\) đồng biến.

+) Với mọi \(x_1, x_2 \in \mathbb{R}\):

TH1: \(0 < x_1 < x_2 \Rightarrow -2x_1 > -2x_2 \Rightarrow f(x_1) > f(x_2)\)

TH2: \( x_1 < 0 < x_2 \Rightarrow -2x_1 > -2x_2 \Rightarrow f(x_1) > f(x_2)\)

TH3: \( x_1 < x_2 < 0 \Rightarrow -2x_1 > -2x_2 \Rightarrow f(x_1) > f(x_2)\)

Vậy trong mọi trường hợp ta đều có: \(x_1, x_2 \in \mathbb{R}\) mà \(x_1 < x_2 \Rightarrow f(x_1) > f(x_2)\).

Do đó hàm số \(y = -2x\) nghịch biến.

Cách 2:

Lập bảng giá trị cho \(x\) nhận các giá trị \(-2; -1; 0; 1; 2\) ta được bảng sau:

Quan sát bảng trên ta thấy: Khi \(x\) càng tăng thì giá trị của hàm số \(y=2x\) càng tăng và giá trị của hàm số \(y=-2x\) càng giả. Do đó:

Hàm số \(y = -2x\) nghịch biến, hàm số \(y = 2x\) đồng biến.